Calculus 1

Evaluate $\displaystyle\int\frac{e^{ \ p \ \tan^{-1}(x)}}{1 + x^2} \ dx$

$\int{\frac{e^{arcsin(x)}}{\sqrt{1-x^2}}}dx$

Evaluate the definite integral below

$\displaystyle\int_{-2}^2 \ {x^2 \cos{(\frac{x^3}{8})}} \ dx$

Evaluate the following definite integral

$\displaystyle\int_0^4 \ x \sqrt{x^2 + 9} \ dx$

Find the area under the curve over the interval $[0,4]$

$f(x) = x^2 + 1$

Find the area under the curve over the interval $[1,4]$

$f(x) = \frac{2}{x}$

Evaluate the integral

$\displaystyle\int_0^2 (2x - 2x^2) \ dx$

Prove the fundamental theorem of calculus

Evaluate the integral $\displaystyle\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} (2 - \csc^2{x}) \ dx$

Find the area the region bounded by:

$y = 1 + \sqrt[3]{x}$

$x = 0$

$x = 8$

$y = 0$

Compute the definite integrals

$\displaystyle\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \tan (x) \ dx$ and $\displaystyle\int_{\frac{-\pi}{3}}^{\frac{\pi}{3}} \tan (x) \ dx$

Find the area between the two curves $y = x^4 - 2x^2$ and $y = 2x^2$

Find the area bounded by the following curves/lines

$y = x + 1$

$y = 9 - x^2$

$x = -1$

$x = 2$

Find the area between the curves $y = x$ and $y = x^2$

Compute the area between $y = \sin{x}$ and $y = \cos{x}$ and the interval $[\frac{\pi}{4}, \frac{5\pi}{4}]$

Compute the area of the region bounded by the curves $y = x^3$ and $y = 3x - 2$

Find the average value on $[0, 16]$ of $f(x) = \sqrt{x}$

What is the average value of the function $f(x) = 3x^2 - 2x$ on $[1, 4]$

Find the average value of the function $h(x) = \cos^4{(x)}\sin(x)$ on $[0, \pi]$

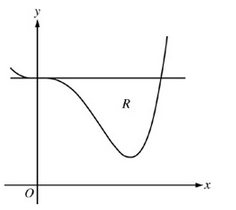
Let R be the region enclosed by the graph of $f(x) = x^4 - 2.3x^3 + 4$ and the horizontal line y = 4, as shown in the figure above.

A. Find the volume of the solid generated when R is rotated about the horizontal line y = -2

B. Region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in R. Find the volume of the solid.

C. The vertical line x = k divides R into two regions with equal areas. Write, but do not solve, an equation involving integral expressions whose solution gives the value k.