Average Value of a Function Problem
Find the average value of the function on
Posted by Ryan Burke a year ago
Related Problems
Find the area between the curves and
Compute the area between and and the interval
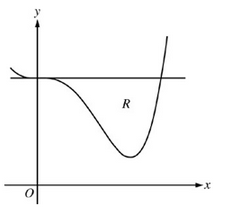
Let R be the region enclosed by the graph of and the horizontal line y = 4, as shown in the figure above.
A. Find the volume of the solid generated when R is rotated about the horizontal line y = -2
B. Region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in R. Find the volume of the solid.
C. The vertical line x = k divides R into two regions with equal areas. Write, but do not solve, an equation involving integral expressions whose solution gives the value k.