AP Calculus Area and Volume Problem

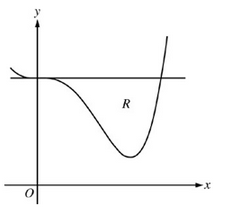
Let R be the region enclosed by the graph of $f(x) = x^4 - 2.3x^3 + 4$ and the horizontal line y = 4, as shown in the figure above.

A. Find the volume of the solid generated when R is rotated about the horizontal line y = -2

B. Region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in R. Find the volume of the solid.

C. The vertical line x = k divides R into two regions with equal areas. Write, but do not solve, an equation involving integral expressions whose solution gives the value k.

For this problem, we're looking at the region R defined by the curve of the function $f(x) = x^4 - 2.3x^3 + 4$ and the horizontal line y = 4. The goal is to explore the volume of solids generated by revolving this region or slicing it in specific ways. Let's break down each part.

Part A asks for the volume of the solid generated when region R is rotated around the horizontal line y = -2. In problems involving rotation, the washer method is commonly used. The washer method involves calculating the volume of disks or washers stacked along an axis. For this case, the distance between the curve and the axis of rotation changes as you move along the x-axis, so you'll need to set up an integral where the radius of each washer is determined by the distance between the function f(x) and the line y = -2. The outer radius would be the distance between y = 4 and y = -2, while the inner radius would be the distance between f(x) and y = -2. After calculating the volumes of these washers, you integrate over the region to get the total volume.

Part B involves using region R as the base of a solid where each cross section perpendicular to the x-axis is an isosceles right triangle with one leg in R. In this case, the key is understanding that the area of each triangle depends on the length of the leg, which corresponds to the height of the region at each x-value (i.e., the vertical distance between f(x) and the line y = 4). The area of an isosceles right triangle is one-half the square of its leg length. To find the volume of the solid, you'll need to set up an integral where you integrate the area of the triangular cross-sections along the x-axis over the range where R exists.

Part C asks for an equation to find the vertical line x = k that divides R into two regions of equal area. This part is an application of setting up an area equation where the integral of the area from the lower bound of R up to x = k is equal to half of the total area of the region. Essentially, you will be solving for k by equating the integral of the function f(x) from the starting x-value of the region to k with half of the total area of R. You won’t solve this equation here but writing it out as an integral will give you the foundation for finding the dividing point.

Each part of this problem involves a unique technique in calculus: the washer method for rotation, calculating volumes based on cross-sections, and setting up integrals to find areas. These techniques are fundamental in understanding how to analyze regions and solids in calculus.

Related Problems