Calculus 1

For the following function, find the first derivative

$\theta = \frac{\tan^{-1}(2r)}{\pi{r}}$

Find the derivative of the following hyperbolic function

$f(x) = \sin{(\sinh{(x)})}$

Find the derivative of $f(x) = {(\sinh^{-1}(x))}^{\frac{3}{2}}$

Find the derivative of $\sinh{(x)}$ and $\cosh{(x)}$

Find the derivative of $\tanh{(3^{x^2} + 4x)}$

A 20 foot ladder is leaning against a wall and the base of the ladder is sliding away at 6 feet a second. How fast is the top of the ladder sliding down the wall when the base of the ladder is 12 feet from the wall?

Let $y = 2(x^2 - 3x)$

a. Find $\frac{dy}{dt}$ when $x = 3$ given $\frac{dx}{dt} = 2$

b. Find $\frac{dx}{dt}$ when $x = 1$ given $\frac{dy}{dt} = 5$

Let $y = \sin{(x)}$

Find $\frac{dy}{dt}$ when $x = \frac{\pi}{4}$ given $\frac{dx}{dt} = 2 \frac{cm}{sec}$

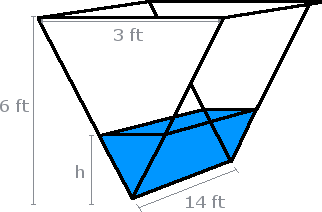
A 10 by 6 foot rectangular swimming pool is being filled. Find the rate at which the height of the water rises if the hose is pouring at $20 \frac{{ft}^3}{hour}$

Find the rate of change of the height of the water level if the hose is pouring $2 \frac{{ft}^3}{m}$

A man is walking away from a lamp at $5 \frac{ft}{s}$

a. Find the rate at which the tip of his shadow is changing

b. Find the rate at which the length of his shadow is changing

A street light is at the top of a 16 ft tall pole. A woman 6 ft tall walks away from the pole with speed of 4 ft/sec along a straight path. How fast is the tip of her shadow moving when she is 35 ft from the base of the pole?

A boat is pulled in by means of a winch on a dock 12 ft above the deck of the boat. If the winch pulls in rope at the rate of 4 ft/sec, determine the speed of the boat when 13 feet of rope is out.

A cylindrical water tank with a radius of 4 meters is being filled with water at a constant rate of 2 cubic meters per minute. Find the rate at which the water level is rising when the water is 3 meters deep.

A man 6 ft tall is walking away from a streetlight 20ft high at a rate of 5ft/sec. At what rate is the tip of his shadow moving when he is 24 feet from the lightpost and at what rate is the length of his shadow increasing?

A kite 100 ft above the ground moves horizontally at a speed of 8 ft/s. At what rate is the angle between the string and the horizontal decreasing when 200 ft of string has been let out?

During a night run, an observer is standing 80 feet away from a long, straight fence when she notices a runner running along it, getting closer to her. She points her flashlight at him and keeps it on him as he runs. When the distance between her and the runner is 100 feet, he is running at 9 feet per second. At this moment, at what rate is she turning the flashlight to keep him illuminated? Include units in your answer.

An airplane is flying at an altitude of 7 miles and passes directly over a radar antenna as shown in the figure. When the plane is 10 miles from the antenna, the radar detects that the distance between the plane and the tower is changing at the rate of 300 mph. What is the speed of the airplane at that moment?

Use the function $f(x) = -x^2 + 3x + 10$ to answer the following: a. On the interval [2,6], what is the average rate of change?

b. On the interval (2,6), when does the instantaneous rate of change equal the average rate of change?

For the following function, use logarithmic differentiation to find $\frac{dy}{dx}$

$y = \frac{{(x + 2)}^2}{\sqrt{x^2 + 1}}$