Evaluate ∫ e p tan − 1 ( x ) 1 + x 2 d x \displaystyle\int\frac{e^{ \ p \ \tan^{-1}(x)}}{1 + x^2} \ dx ∫ 1 + x 2 e p t a n − 1 ( x ) d x
∫ e a r c s i n ( x ) 1 − x 2 d x \int{\frac{e^{arcsin(x)}}{\sqrt{1-x^2}}}dx ∫ 1 − x 2 e a rcs in ( x ) d x
Evaluate the definite integral below
∫ − 2 2 x 2 cos ( x 3 8 ) d x \displaystyle\int_{-2}^2 \ {x^2 \cos{(\frac{x^3}{8})}} \ dx ∫ − 2 2 x 2 cos ( 8 x 3 ) d x
Evaluate the following definite integral
∫ 0 4 x x 2 + 9 d x \displaystyle\int_0^4 \ x \sqrt{x^2 + 9} \ dx ∫ 0 4 x x 2 + 9 d x
Find the area under the curve over the interval [ 0 , 4 ] [0,4] [ 0 , 4 ]
f ( x ) = x 2 + 1 f(x) = x^2 + 1 f ( x ) = x 2 + 1
Find the area under the curve over the interval [ 1 , 4 ] [1,4] [ 1 , 4 ]
f ( x ) = 2 x f(x) = \frac{2}{x} f ( x ) = x 2
Evaluate the integral
∫ 0 2 ( 2 x − 2 x 2 ) d x \displaystyle\int_0^2 (2x - 2x^2) \ dx ∫ 0 2 ( 2 x − 2 x 2 ) d x
Prove the fundamental theorem of calculus
Evaluate the integral ∫ π 4 π 2 ( 2 − csc 2 x ) d x \displaystyle\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} (2 - \csc^2{x}) \ dx ∫ 4 π 2 π ( 2 − csc 2 x ) d x
Find the area the region bounded by:
y = 1 + x 3 y = 1 + \sqrt[3]{x} y = 1 + 3 x
x = 0 x = 0 x = 0
x = 8 x = 8 x = 8
y = 0 y = 0 y = 0
Compute the definite integrals
∫ π 6 π 3 tan ( x ) d x \displaystyle\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \tan (x) \ dx ∫ 6 π 3 π tan ( x ) d x ∫ − π 3 π 3 tan ( x ) d x \displaystyle\int_{\frac{-\pi}{3}}^{\frac{\pi}{3}} \tan (x) \ dx ∫ 3 − π 3 π tan ( x ) d x
Find the area between the two curves y = x 4 − 2 x 2 y = x^4 - 2x^2 y = x 4 − 2 x 2 y = 2 x 2 y = 2x^2 y = 2 x 2
Find the area bounded by the following curves/lines
y = x + 1 y = x + 1 y = x + 1
y = 9 − x 2 y = 9 - x^2 y = 9 − x 2
x = − 1 x = -1 x = − 1
x = 2 x = 2 x = 2
Find the area between the curves y = x y = x y = x y = x 2 y = x^2 y = x 2
Compute the area between y = sin x y = \sin{x} y = sin x y = cos x y = \cos{x} y = cos x [ π 4 , 5 π 4 ] [\frac{\pi}{4}, \frac{5\pi}{4}] [ 4 π , 4 5 π ]
Compute the area of the region bounded by the curves y = x 3 y = x^3 y = x 3 y = 3 x − 2 y = 3x - 2 y = 3 x − 2
Find the average value on [ 0 , 16 ] [0, 16] [ 0 , 16 ] f ( x ) = x f(x) = \sqrt{x} f ( x ) = x
What is the average value of the function f ( x ) = 3 x 2 − 2 x f(x) = 3x^2 - 2x f ( x ) = 3 x 2 − 2 x [ 1 , 4 ] [1, 4] [ 1 , 4 ]
Find the average value of the function h ( x ) = cos 4 ( x ) sin ( x ) h(x) = \cos^4{(x)}\sin(x) h ( x ) = cos 4 ( x ) sin ( x ) [ 0 , π ] [0, \pi] [ 0 , π ]
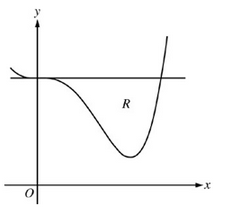
Let R be the region enclosed by the graph of f ( x ) = x 4 − 2.3 x 3 + 4 f(x) = x^4 - 2.3x^3 + 4 f ( x ) = x 4 − 2.3 x 3 + 4
A. Find the volume of the solid generated when R is rotated about the horizontal line y = -2
B. Region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in R. Find the volume of the solid.
C. The vertical line x = k divides R into two regions with equal areas. Write, but do not solve, an equation involving integral expressions whose solution gives the value k.