Find the derivative of y = tan ( 2 x ) x 2 y = \frac{\tan{(2x)}}{x^2} y = x 2 t a n ( 2 x )
Use the definition of e e e lim h → 0 e h − 1 h = 1 \lim_{h\rightarrow 0}\frac{e^{h} - 1}{h} = 1 lim h → 0 h e h − 1 = 1 f ( x ) = e x f(x) = e^x f ( x ) = e x e x e^x e x
Determine the derivative of f ( x ) = 2 x 5 − 3 e 6 x f(x) = 2x^5 - 3e^{6x} f ( x ) = 2 x 5 − 3 e 6 x
Use logarithmic differentiation to find the derivative in the following example
g ( x ) = log 3 ( 2 x 2 − 5 x ) g(x) = \log_{3}(2x^{2} - 5x) g ( x ) = log 3 ( 2 x 2 − 5 x )
Use the chain rule to find the derivative of the following function
f ( x ) = 3 x 3 + 10 x f(x) = \sqrt{3x^3 + 10x} f ( x ) = 3 x 3 + 10 x
Find the derivative of f ( x ) = 2 5 x 2 + 3 x f(x) = \frac{2}{5x^2 + 3x} f ( x ) = 5 x 2 + 3 x 2
Given y = 4 ( 3 x + 4 ) 5 y = 4 (3x + 4)^5 y = 4 ( 3 x + 4 ) 5 d y d x \frac{dy}{dx} d x d y
Find d y d x \frac{dy}{dx} d x d y x 3 + 3 y 4 = 2 x + 7 x^3 + 3y^4 = 2x + 7 x 3 + 3 y 4 = 2 x + 7
For the following equation, differentiate implicitly to find d y d x \frac{dy}{dx} d x d y
e ( x + y ) = sin ( x ) + cos ( y ) e^{(x + y)} = \sin{(x)} + \cos{(y)} e ( x + y ) = sin ( x ) + cos ( y )
Determine the first and second derivatives, d y d x \frac{dy}{dx} d x d y d 2 y d x 2 \frac{d^{2}y}{dx^2} d x 2 d 2 y
x 2 + x y = 4 x^2 + xy = 4 x 2 + x y = 4
Show that d d x ( arcsin x ) = x ′ 1 − x 2 \frac{d}{dx}(\arcsin{x}) = \frac{x^{\prime}}{\sqrt{1 - x^2}} d x d ( arcsin x ) = 1 − x 2 x ′
Determine the derivative of the following inverse trig function
f ( x ) = arctan ( x ) f(x) = \arctan{(\sqrt{x})} f ( x ) = arctan ( x )
Determine the derivative of the inverse trigonometric function
f ( x ) = sec − 1 ( 5 x ) f(x) = \sec^{-1}{(5x)} f ( x ) = sec − 1 ( 5 x )
Find the derivative of f ( x ) = 2 arccos ( x 3 ) f(x) = 2\arccos{(\frac{x}{3})} f ( x ) = 2 arccos ( 3 x )
Find the derivative of sinh ( x ) \sinh{(x)} sinh ( x ) cosh ( x ) \cosh{(x)} cosh ( x )
Find the derivative of tanh ( 3 x 2 + 4 x ) \tanh{(3^{x^2} + 4x)} tanh ( 3 x 2 + 4 x )
A 10 by 6 foot rectangular swimming pool is being filled. Find the rate at which the height of the water rises if the hose is pouring at 20 f t 3 h o u r 20 \frac{{ft}^3}{hour} 20 h o u r f t 3
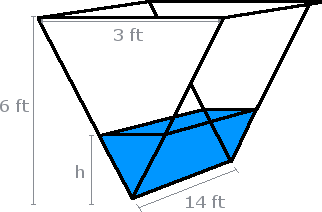
Find the rate of change of the height of the water level if the hose is pouring 2 f t 3 m 2 \frac{{ft}^3}{m} 2 m f t 3
A man is walking away from a lamp at 5 f t s 5 \frac{ft}{s} 5 s f t
a. Find the rate at which the tip of his shadow is changing
b. Find the rate at which the length of his shadow is changing
A street light is at the top of a 16 ft tall pole. A woman 6 ft tall walks away from the pole with speed of 4 ft/sec along a straight path. How fast is the tip of her shadow moving when she is 35 ft from the base of the pole?