Physics 1

A small block of mass MB= 0.50 kg is placed on a long slab of mass MS= 3.0 kg as shown below. Initially, the slab is at rest and the block has a speed v0of 4.0 m/s to the right. The coefficient of kinetic friction between the block and slab is 0.20, and there is no friction between the slab and the horizontal surface on which it moves.

A box is being pulled with force Fa= 40 N at an angle θ= 30 degrees. There is a frictional force opposing the sliding of the box with force Ff= 10 N. Draw a free body diagram to help answer the following questions. (use gravity at 10m/s2 to simplify the numbers)

A 5 kg lawn mower is being pushed with an applied force of Fa= 20 N, at an angle of θ. There is a frictional force, F$_f$ opposing the movement of the lawn mower of 10 N. Given that the lawn mower is accelerating at 0.4 m/s$^2$:

A block of mass mis pulled along a rough horizontal surface by a constant applied force of magnitude F1that acts at an angle θto the horizontal, as indicated below. The acceleration of the block is a1. Express all algebraic answers in terms of m, F1, θ, a1, and fundamental constants.

A rubber ball of mass m is dropped from a cliff. As the ball falls, it is subject to air drag (a resistive force caused by the air). The drag force on the ball has a magnitude bv2, where bis a constant drag coefficient and v is the instantaneous speed of the ball. The drag coefficient bis directly proportional to the cross-sectional area of the ball and the density of the air and does not depend on the mass of the ball. As the ball falls, its speed approaches a constant value called the terminal speed.

Draw and label all the forces on the ball at some instant before it reaches terminal speed.

State whether the magnitude of the acceleration of the ball of mass m increases, decreases, or remains the same as the ball approaches terminal speed. Explain.

Write, but do NOT solve, a differential equation for the instantaneous speed vof the ball in terms of time t, the given quantities, and fundamental constants.

Determine the terminal speed vtin terms of the given quantities and fundamental constants.

Determine the energy dissipated by the drag force during the fall if the ball is released at height hand reaches its terminal speed before hitting the ground, in terms of the given quantities and fundamental constants. (this question requires knowledge of potential and kinetic energy, often not introduced until later in a physics course)

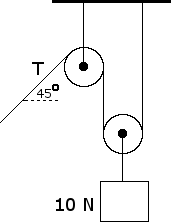
What is the tension T in the rope if the 10-N weight is moving upward with a constant velocity?

A car of mass 100 kg is traveling in a circle of radius 20 m. There is a frictional force of 500 N on the car's wheels (in the direction of the center of the circle, to keep the car going in a circle). Draw a free body diagram for the car and find the velocity of the car.

A student is swinging a mass, m = 2.0 kg, in a uniform vertical circle of radius R = 2.5 m. The period of the rotation is 2.8 seconds. Draw a free body diagram for the mass at the top of the circle and find the tension of the string (ignore friction and the mass of the string.) Repeat for the mass at the bottom of the rotation.

A car is driving in a circle on an embanked road as shown below. Draw a free body diagram for the car, ignoring friction.

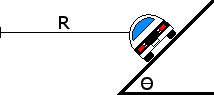
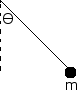
A 1.2 kg mass, m, is swinging on a string pendulum of length 80 cm (the string has negligible mass). As shown in the figure below, when $\theta$ is 10 degrees the velocity of the mass is 0.6 m/s. Find the tension in the string and the acceleration of the mass at this moment.

Given that the radius of orbit for the moon is 3.8 x 10$^8$ m, the period of the moon's orbit is 2.36 x 10$^6$ s, and the radius of the earth is 6.38 x 10$^6$ m; Find the altitude of a geostationary satellite.(hint: use Kepler's third law.)

Find the period of a satellite at an altitude of 200 km.

R$_E$ = 6.38 x 10$^6$ m

M$_E$ = 5.98 x 10$^{24}$ kg

G = 6.67 x 10$^{-11}$ $\frac{Nm^2}{kg^2}$

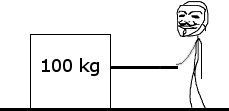
The 100 kg box shown below is being pulled along the x-axis by a student. The box slides across a rough surface, and its position $x$ varies with time $t$ according to the equation $x = 0.5t^3 + 2t$ , where $x$ is in meters and $t$ is in seconds.

C. Calculate the net work done on the box in the interval $t$ = 0 to $t$ = 2 s would be greater than, less than, or equal to the answer in part (C). Justify your answer.

The figure below depicts a roller coaster. Assume the roller coaster starts at a velocity of 0 m/s from 70 m.

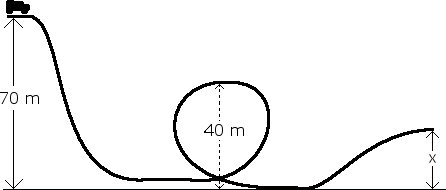
B. Determine the height of the track at point x. It is known that the roller coaster has a velocity of 30 m/s at x.

A 20 kg student is about to go down a slide. There is a 3 N frictional force opposing his movement. Assume his velocity at the top of the slide is 0 m/s. Find his velocity at the bottom of the slide.

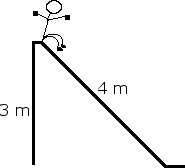
A student is about to be launched from a spring loaded canon. The student weighs 60 kg and the spring constant is 200 N/kg. Find the students velocity the moment he leaves the canon if the spring is compressed, x = 3 m. Also find the students velocity after the spring has decompressed to x = 2 m.

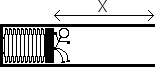
A marble, m, of mass 100 g is placed onto a platform attached to a spring. The weight of the marble compresses the spring 2 cm, as shown below. A force is then applied to the platform to compress the spring an additional 3 cm. When the force is taken away, the spring decompresses and launches the marble upward. What is the maximum height the marble obtains above the unstretched spring (the spring with no mass on it).

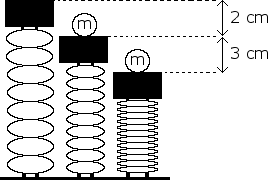
A nonlinear spring is compressed various distances x, and the force Frequired to compress it is measured for each distance. The data are shown in the table below.

In an experiment to determine the spring constant of an elastic cord of length 0.60 m, a student hangs the cord from a rod and then attaches a variety of weights to the cord. For each weight, the student allows the weight to hang in equilibrium and then measures the entire length of the cord. The data are recorded in the table below:

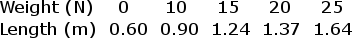
iii. Calculate the maximum speed of the object.

A rubber ball of mass $m$ is dropped from a cliff. As the ball falls, it is subject to air drag (a resistive force caused by the air). The drag force on the ball has a magnitude $bv^2$ , where $b$ is a constant drag coefficient and $v$ is the instantaneous speed of the ball. The drag coefficient $b$ is directly proportional to the cross-sectional area of the ball and the density of the air and does not depend on the mass of the ball. As the ball falls, its speed approaches a constant value called the terminal speed.

A. Draw and label all the forces on the ball at some instant before it reaches terminal speed.

B. State whether the magnitude of the acceleration of the ball of mass $m$ increases, decreases, or remains the same as the ball approaches terminal speed. Explain.

C. Write, but do NOT solve, a differential equation for the instantaneous speed $v$ of the ball in terms of time $t$ , the given quantities, and fundamental constants.

D. Determine the terminal speed $v_t$ in terms of the given quantities and fundamental constants.

E. Determine the energy dissipated by the drag force during the fall if the ball is released at height $h$ and reaches its terminal speed before hitting the ground, in terms of the given quantities and fundamental constants.